Introduction:

Binary trees are hierarchical data structures commonly used in computer science and programming. They consist of nodes connected by edges, where each node can have at most two children: a left child and a right child. Binary trees are extensively used for efficient searching, sorting, and organizing data.

There are different ways to implement binary trees, and one popular approach is the array-based implementation. In this implementation, the binary tree is represented using an array, which provides easy access to nodes based on their indices. The array is typically organized in a way that reflects the hierarchical structure of the binary tree.

To implement a binary tree using an array, we assign indices to the nodes based on their level and position within that level. The root node is assigned index 0, and for any node at index 'i', its left child is located at index '2i + 1', and its right child is located at index '2i + 2'. Conversely, for any node at index 'i', its parent is located at index '(i-1)/2'.

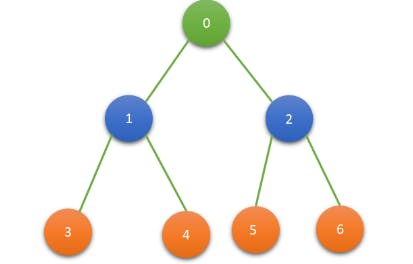
The corresponding array representation would be: [10,1,2,3,4,5,6]. In this representation, the root node '1' is at index 0, its left child '2' is at index 1, its right child '3' is at index 2, and so on.

The array-based implementation provides advantages in terms of memory efficiency and simplicity of access, especially when the binary tree is complete (i.e., every level, except possibly the last, is completely filled) or nearly complete. However, it can be less efficient for dynamic operations such as inserting or deleting nodes, as it requires shifting elements in the array.

#include<iostream>
using namespace std;
class tree//Create class
{
  private://Private no need becouse all functionality useing public
  public://All attribute public
  char tree[10];//Array declaraction
  void addroot(char data)//Add rooter data
  {
      tree[0]=data;//Enter a data 0 index
  }

  void add_left( char data,int p)// Add leftside  odd indexes function with parameter
  {
      if(tree[p]=='\0')//Check condition parent node null or not
      {
          cout<<"Parient not exist "<<endl;//print
      }
      else
      {
          tree[(p*2)+1]=data;//Use formula left side odd indexes 
      }
  }

  void add_right( char data,int p)// Add rightside  even indexes function with parameter
  {
      if(tree[p]=='\0')//Check condition parent node null or not
      {
          cout<<"Parient not exist "<<endl;//print
      }
      else
      {
          tree[(p*2)+2]=data;;//Use formula right side even indexes 
      }
  }
  void display()// Function display all nodes data 
  {
      for(int i=0;i<10;i++)//forloop
      {
          cout<<tree[i]<<endl;//print
      }
  }
};

int main()
{
    tree t1;//Create object
    t1.addroot('A');//Rooter (main)node data... 
    t1.add_left('B',0);// Data enter left side odd index 
    t1.add_right('C',0);//Data enter right side even index 

    t1.add_left('D',1);// Data enter left side odd index 
    t1.add_right('E',1);//Data enter right side even index 

    t1.add_left('F',2);;// Data enter left side odd index 
    t1.add_right('G',2);//Data enter right side even index 
    t1.display();//Call display function


}

It's important to note that while the array-based implementation provides a convenient way to store and access binary tree nodes, it is not the only way to implement binary trees. Other implementations, such as linked structures using pointers or references, may be more suitable for certain scenarios depending on the specific requirements of the application.